IOptlib
This page provides some
information about the Ioptlib (Investigative Optimization
Library), whose experimental version
release is planned for 2008.
|
|
About the library
Ioptlib (the Investigative Optimization Library)
is an optimization library for developing and testing algorithms for
solving engineering optimization problems. A priority goal is to
develop algorithms suited to problems with computationally expensive
and possibly noisy evaluation of the response (i.e. objective and
constraint) functions. The library is intended to provide modular
building blocks for constructing such algorithms, standardized
templates for interfacing tools obtained form other libraries, and
testing environment where different performance aspects of
algorithms can be readily extensively tested during and after the
development stage. Currently most of the efforts are devoted to
algorithms based on successive solution of approximated problems
obtained by local sampling and approximation of the response
functions. Such algorithms have complex designs and involve solution
of many sub-problems such as non-linear or quadratic programming
problems, matrix algebra, optimal sampling strategies, etc. The
intention is therefore to gradually accumulate efficient routines
for solving these problems, which will lead to broader
serviceability of the library. Any attempt was made to keep open the
possibility of starting development of new algorithms or attaching
to the existent functionality at any level. The basic library is
therefore intended to be distributed as free open source under
certain conditions. A couple of algorithms will be available under
different negotiable terms since this is necessary to provide the
funding for library development, however their building blocks
together with a set of quite useful algorithms will be provided with
the basic set that is more open what concerns availability.
The original motivation for the library was obtained in
optimization of forming processes where evaluation of objective and
constraint functions typically involves complex numerical simulation
with hundreds of thousands of degrees of freedom, very non-linear
and path dependent materials, multi-physics and multi-scale
phenomena etc. As result, not only the calculation of the objective
and constraint functions takes very long times even on the fastest
computers or parallel architectures, but these functions often
contain substantial amount of numerical noise. These conditions
impose a substantial turn in how algorithm performance is viewed. On
one hand the most important measure of algorithm efficiency becomes
the number of function evaluations it takes for calculating optimum
up to a given accuracy. The CPU time spent by the algorithm becomes
somehow less important because function evaluations will normally
require incomparably more computational time. Because running
optimization procedures will often be just on the limit of
affordable, the goal will not always be to find an optimal solution
up to a specified accuracy, but rather to achieve significant
improvement within affordable computational time.
The targeted scope of the library is beyond the area of its
original motivation. It is intended to provide a pool of algorithms
for different problems and facilities for extending this pool.
Beside that, interaction with other libraries and use of the library
in existing or future software is accounted for as much as possible.
A lot of stress is put on defining standard data types and function
prototypes used for different purposes, such as evaluation of
response functions and their derivatives or for storing results of
such evaluation and their use in building approximations. These
standards are defined in such a way that routines for similar tasks
from other libraries can be easily incorporated in the system, and
functions that are consistent with library standards can be easily
exported in standard forms required in other software environments.
Wrapping functions and data converters are provided for some common
cases, and the way how one can create own tools for this is being
documented in manuals. The standards are designed in such a way that
they are suitable for any environment, in particular to allow
recursive calls and work in multi-threaded environment.
The library comes with a set of basic utilities that are
extensively used in implementation of basic building blocks and
algorithms. This includes e.g. basic matrix and vector operations
and generic implementation of data containers such as stacks. These
utilities are well documented in source code while overview is given
in documentation.
Many of elementary utilities make use of other free
libraries. Contribution of people who designed these libraries and
made them available is gratefully acknowledged.
Availability
The library has been released experimentally June 2008. It
was initially planned that the library would be incorporated in
the optimization software Inverse as its base
library. However, this development did not continue after 2007,
but the software still uses numerous routines from the library.
The library was released publicly in order to promote the exchange
of ideas between researchers working on similar problems in
optimization. Since 2007, the development has migrated completely
to a more general purpose IGLib.NET
framework library, which is actively developed and is based mainly
on the .NET platform. A large portion of optimization algorithms
and utilities has been transferred to that platform (some of it
still in the sandbox section), or it is planned to be transferred.
Documentation
IOptLib
User's Manual. This manual is mainly intended for users of the
library, however the extent of information is sufficient that it cna
be advantageously used by developers.
Simplex algorithms for nonlinear
constraint optimization problems. This documents
containd description of a set of modified Nelder-Mead simplex
algorithms that can be used for constraint nonlinear optimization.
These algorithms can beadvantageously used for optimization
when gradients of the objective and constraint functions are not
available and where these functions are not smooth. All the
described algorithms are implemented in IOptLib.
See also:
Example: optimization by
using successive approximations of response
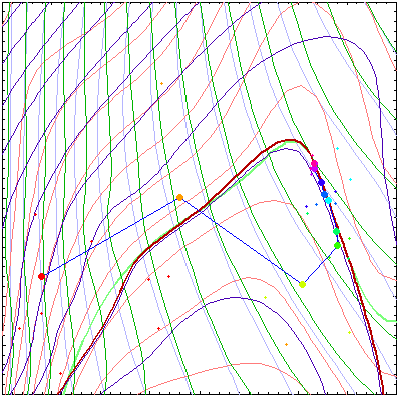
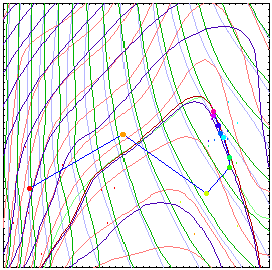
This figure represents convergence of an algorithm
based on successive approximation of the response functions.
Contours of actual objective and constraint function are shown in
pale colors while contours of approximated functions are
plotted in stronger colors. Zero constraint contours (actual and
approximated) are plotted with thicker lines. Small points are the
sampling points where the response functions (loaded with some level
of noise) were calculated, and larger points are the solutions of
the approximated problems.
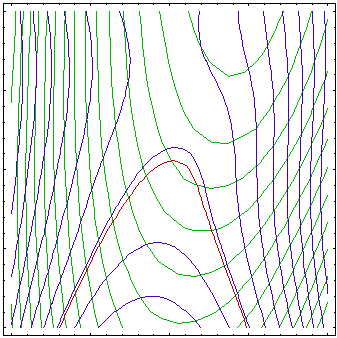
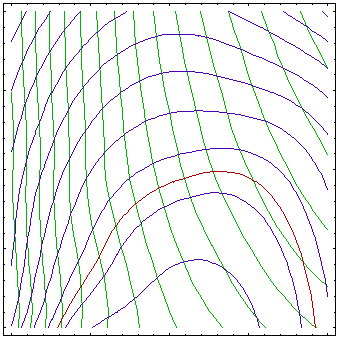
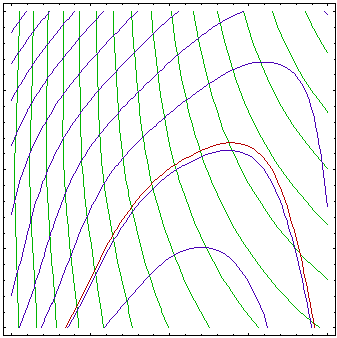
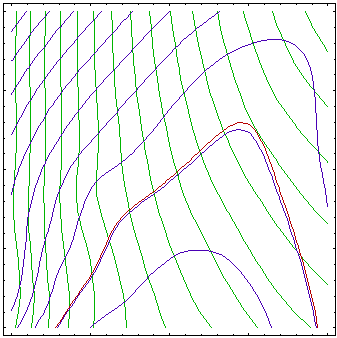
The figure above shows approximations of the objective (green
contours) and constraint functions (blue contours, brown 0 contour)
after 1, 3, 6 and 10 iterations of an algorithm based on successive
approximations. First, the approximations are very rough, with
better approximation around the initial point. Over iterations,
center of the approximated region moves towards optimum (see Figure
above) and approximation gets better around the optimum while region
far from optimum is not of interest and is not well approximated.
Updated in September 2008
|
Number of accesses: 
If you don't see
the access counter properly then please follow this
link!