Equilibrium
States of Charged Particles in a Two-dimensional Circular Region
Problem description
The force between two charged particles is governed by the Coulomb law:
![]() (1)
(1)
The potential energy of a system of N charged particles has the following form:
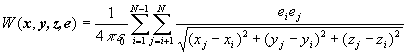 (2)
(2)
If the potential
energy W has one or more minima
then the existence of the equilibrium state(s) is assured. If the particle
charges are prescribed (constants) then the potential energy of the system
depends on 3N parameters p (x,y and z coordinates of
the particles). The aim of the optimization is to find at least one of the
minima of the potential energy function W(p) for the cases that include various
geometric constraints of the
form:
![]() (3)
(3)
![]() (4)
(4)
where E and I are subsets of {1,2,..,3N-1,3N}.
Definition of the optimization
problem
Let us assume that N equal unit-charged
particles are kept in a planar circular region. Because of the axial symmetry
of the case the potential energy of the system and its geometrical constraints
can be expressed in terms of cylindrical coordinates:
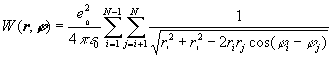 (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
The constraint zi=0 is already taken into the account in the equation (5). Our task is to find the equilibrium states of such a system of N charged particles. Potential energy depends on 2N parameters ri and ji.
Optimization is started at random distribution of particles. It is done by gradient method which requires calculation of the sensitivities. Sensitivities are partial derivatives of the objective function with respect to coordinates ri and ji:
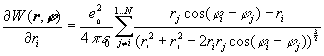 (5)
(5)
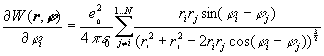 (6)
(6)
Results
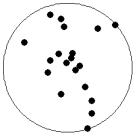
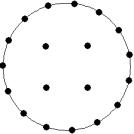
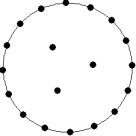
At small number of particles it can be expected that in the equilibrium state they will be located along the circular region boundary. From certain number of particles on equilibrium states with particles located in the interior of the region can be expected too. The values of the potential energy at different equilibrium states of the system are presented in table 1. Numbers in brackets indicate the number of particles lying in the interior of the region as seen on figures 1-18. The number of possible equilibrium states is rising with N. Calculated optimal distributions depend on initial particle distributions. The values of potential energy (Wo) in the second column (presumably optimal) were calculated by optimizations starting from symmetrical particle distribution with appropriate number of particles lying in the interior of the region.
|
N |
Wr |
Wo |
N |
Wr |
Wo |
|
2 |
0.5000000 (0) |
0.5000000 (0) |
11 |
49.909625 (1) |
48.575675 (0) |
|
3 |
1.7320508 (0) |
1.7320508 (0) |
12 |
59.575675 (1) |
59.575675 (1) |
|
4 |
3.8284272 (0) |
3.8284272 (0) |
13 |
72.706597 (2) |
71.807362 (1) |
|
5 |
7.8284271 (1) |
6.8819100 (0) |
14 |
86.002080 (2) |
85.347290 (1) |
|
6 |
10.964102 (0) |
10.964102 (0) |
15 |
101.67726 (3) |
100.220965 (1) |
|
7 |
16.964102 (1) |
16.133354 (0) |
16 |
117.37000 (3) |
116.452000 (1) |
|
8 |
23.133354 (1) |
22.438927 (0) |
17 |
134.38698 (3) |
133.816520 (2) |
|
9 |
30.438927 (1) |
29.923449 (0) |
18 |
152.75425 (3) |
152.477900 (2) |
|
10 |
38.923449 (1) |
38.624499 (0) |
19 |
173.38325 (4) |
172.494820 (3) |
Table 1: Potential energy for different equilibrium states of the system
Appendix (Figures of equilibrium
states)
2
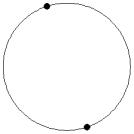
3
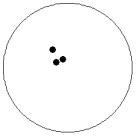
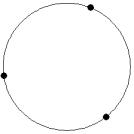
4
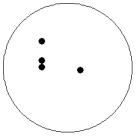
5
6
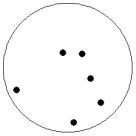
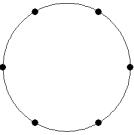
7

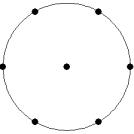
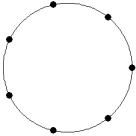
8
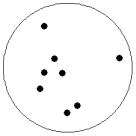
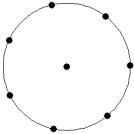
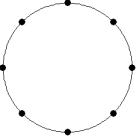
9

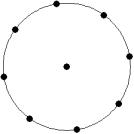
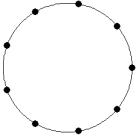
10
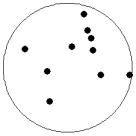
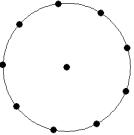
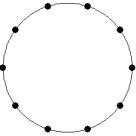
11

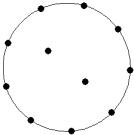
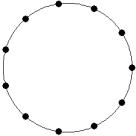
12
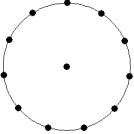
13

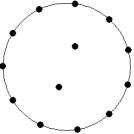
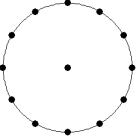
14
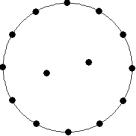
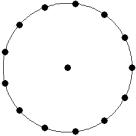
15
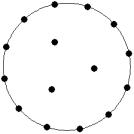
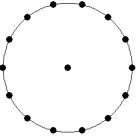
16

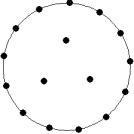
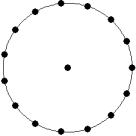
17
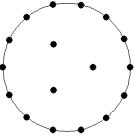
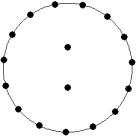
18

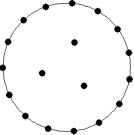
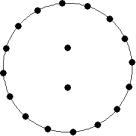
19